인덱스 트리 (Binary Indexed Tree)

1. 정의

인덱스 트리는 원소들의 구간 합을 빠르게 구하기 위해 사용하는 자료구조로 펜윅 트리라고도 한다. 세그먼트 트리와 같이 기능을 하지만 구현이 좀 더 쉽고 직관적이며 많은 문제에 활용할 수 있다.

인덱스 트리는 원소를 업데이트(Point update)하거나 구간 합(Range query)을 구하는 데 걸리는 시간은 $O(logN)$이다.

2. 구현

1) 배열 크기 설정

인덱스 트리는 포화 이진트리로 먼저 배열의 크기를 구해야 한다. 단순히 배열에 원소만 들어가는 것이 아니라 원소들의 구간합 정보가 배열에 포함되어야 한다.

인덱스 트리의 리프 노드에 원소가 저장이 되어야 하고, 리프 노드부터 루트 노드까지 각각의 부모 노드는 자식 노드들의 합이 저장되어야 한다면 구현에 필요한 노드의 개수 즉, 인덱스 트리의 크기는 최소 몇이어야 할까? 결론부터 말하자면 N개의 원소를 입력받았을 때, 인덱스 트리의 크기는 최소 $2^{\left \lceil log_{2}N\right \rceil+1}-1$개이다.

예를 들어 다음과 같이 4개의 원소 정보를 입력받았다고 해보자.

인덱스 트리의 리프 노드에 원소가 저장이 되어야 한다고 했으므로 다음과 같이 4개의 리프 노드가 존재한다.

그다음 루트 노드까지 부모 노드에 자식 노드들의 합을 저장하면 다음과 같은 인덱스 트리가 만들어진다.

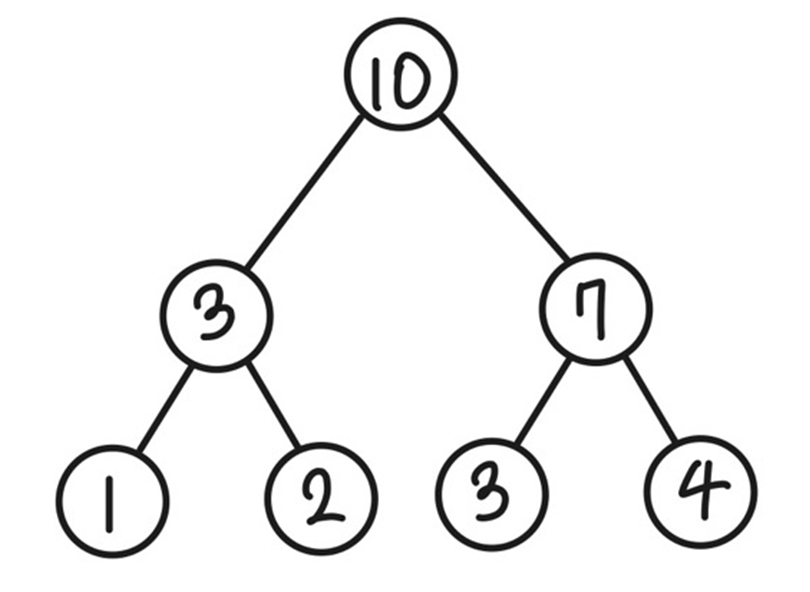
그림에서 볼 수 있듯이 N=4일 때, 노드의 개수는 7개이다.

그럼 만약 N=5 즉, 입력으로 원소 하나가 더 추가가 된다면 노드의 개수는 어떻게 될까? 다시 말하지만 인덱스 트리는 포화 이진트리이므로 다음과 같이 원소가 없는 빈 리프 노드를 가지는 트리가 된다. (빈 리프 노드라고 표현은 했지만, 우리는 구간 합을 구하는 것이 목표이므로 실제로는 0을 저장한다.)

N=4일 때와 비교해 보면, N이 겨우 1 증가했지만 인덱스 트리의 노드는 8개가 증가하여 총 15개가 된 것을 확인할 수 있다.

결론을 도출하기 위해 N에 많은 수를 대입하여 생각해 보자.

N=6일 때는 위와 같이 노드의 개수는 15개일 것이다.

N=7일 때와 8일 때도 마찬가지로 15개일 것이다.

N=9일 때는 15개의 노드로 포화 이진트리를 만들 수 없으므로 더 많은 노드가 필요하다. 이때 노드의 개수를 생각해 보면 아마도 31개일 것이다. 왜냐하면 포화 이진트리를 만족하면서 노드를 추가하려면 결국 트리의 높이를 증가시켜야 한다.

따라서 트리의 높이 $h=\left \lceil log_{2}N\right \rceil$라고 하면 포화 이진트리의 노드의 개수는 $2^{\left \lceil log_{2}N\right \rceil+1}-1$개이다.

사실 나도 수식이 잘 와닿지는 않았는데 좀 쉽게 생각을 한다면 다음과 같이 할 수 있다. N보다 처음으로 크거나 같아지는 2의 제곱수를 $OFFSET$이라는 변수로 둔다면 인덱스 트리의 크기는 2 * $OFFSET$ - 1이다. 그래서 처음부터 인덱스 트리의 크기를 생각하지 말고 $OFFSET$을 잘 설정하면 된다. 위의 예시를 다시 보자. N=9일 때 9보다 처음으로 크거나 같아지는 2의 제곱수는 16이다. 따라서 $OFFSET$이 16이므로 인덱스 트리의 크기는 2 * $OFFSET$ - 1 = 2 * 16 - 1 = 31이다. 너무 쉽다!

그러면 $OFFSET$을 어떻게 구할까? 다음과 같이 간단하게 $OFFSET$을 구할 수 있다.

int OFFSET = 1; // 1부터 시작
while (OFFSET < N) OFFSET *= 2; // N보다 크거나 같아질 때까지 2배

그런데 문제를 많이 풀다 보면 특정 N에 대한 $OFFSET$값이 외워지기도 하고 사실 계산기로도 쉽게 구할 수 있다. 대표적으로 N이 10만 일 때 $OFFSET$은 131,072이고, N이 100만 일 때 $OFFSET$은 1,048,576이다.

$OFFSET$값을 구했다면, 인덱스 트리의 크기 즉, 1차원 배열의 크기도 할당해 주자.

vector<int>tree(OFFSET * 2);

나는 인덱스 트리를 구현할 때 배열의 인덱스를 1부터 시작하는 것을 선호한다. 이 말은 루트 노드의 인덱스를 0이 아니라 1로 놓고 시작한다는 뜻이다. 따라서 실제로 배열을 할당할 때, $OFFSET$ * 2 - 1로 하는 것이 아니라 $OFFSET$ * 2로 설정했다.

2) 배열 초기화

N개의 원소를 입력받고 N에 따라 $OFFSET$도 잘 구해서 tree 배열을 잘 만들었다면 이제 초기화를 해보자. 입력받은 N개의 원소는 리프 노드에 저장되어야 한다고 했다. 그러면 리프 노드들의 인덱스는 몇일까? 생각을 조금만 해보면 아마 $OFFSET$이 처음 리프 노드의 인덱스인 것을 알 수 있다. 루트 노드의 인덱스를 1이라고 했으므로 포화 이진트리의 각 level에서 가장 왼쪽 노드는 항상 2의 제곱수이기 때문이다.

처음 리프 노드의 인덱스가 $OFFSET$인 것을 알았다면 $OFFSET$부터 N개의 노드에 입력받은 N개의 원소를 아래처럼 저장해 보자.

// N개의 원소를 arr 배열에 저장했다고 가정.
for (int i = 0; i < N; i++) tree[i + OFFSET] = arr[i];

배열의 $OFFSET$부터 원소를 저장했다면 이제 루트 노드를 나타내는 1번 노드부터 $OFFSET$ - 1번 노드까지 알맞은 원소를 저장해야 한다. 리프 노드부터 루트 노드까지 bottom-up 방식으로 원소를 채워나가야 하는데 각각의 부모 노드는 자식 원소들을 더한 값이 저장되어야 한다. 여기서 이제 포화 이진트리 즉, 인덱스 트리의 장점이 드러난다. 포화 이진트리에서 부모 노드의 인덱스는 항상 자식 노드의 인덱스에 2를 나눈 값이다. 여기서 말하는 자식 노드는 왼쪽 자식 노드든 오른쪽 자식 노드든 상관이 없다. 예를 들어 왼쪽 자식 노드의 인덱스가 20이고 오른쪽 자식 노드의 인덱스가 21일 때 부모 노드의 인덱스는 int형이므로 20에서 2를 나누든 21에서 2를 나누든지 값은 10으로 똑같기 때문이다.

그러면 반대로 부모 노드의 입장에서 자식 노드를 보자. 부모 노드의 인덱스가 10일 때 왼쪽 자식 노드의 인덱스는 20이고 오른쪽 자식노드의 인덱스는 21이다. 일반화를 해보면 부모 노드의 인덱스가 $i$일 때 왼쪽 자식 노드의 인덱스는 $2*i$이고 오른쪽 자식 노드의 인덱스는 $2*i+1$이다. 이러한 인덱스 트리의 특징을 통해 배열을 쉽게 초기화하고 구간합을 구할 수 있게 된다.

아래와 같이 1번부터 $OFFSET$ - 1번 노드까지 왼쪽 자식 노드와 오른쪽 자식 노드의 원소를 더한 값을 저장해 보자.

for (int i = OFFSET - 1; i >= 1; i--) tree[i] = tree[2 * i] + tree[2 * i + 1];

위의 코드들을 init 함수로 묶자.

void init() {
	// OFFSET부터 OFFSET + N - 1 까지
	for (int i = 0; i < N; i++) tree[i + OFFSET] = arr[i];
    	// 1부터 OFFSET - 1 까지
	for (int i = OFFSET - 1; i >= 1; i--) tree[i] = tree[2 * i] + tree[2 * i + 1];
}

3) Point update

아래와 같은 인덱스 트리가 있다고 해보자. 검은색 숫자는 원소, 파란색 숫자는 인덱스를 나타낸다.

이는 8개의 원소를 입력받았을 때의 인덱스 트리 모습이다. N=8이므로 $OFFSET$은 8보다 처음으로 크거나 같은 2의 제곱수인 8이 될 것이다. 따라서 위 그림처럼 8번 노드부터 15번 노드까지 차례로 원소를 저장하고 루트 노드까지 자식 노드의 합을 저장했다.

1번 노드가 무엇을 나타내는지 살펴보자. 1번 노드는 init 함수에 따라 왼쪽 자식 노드인 2번 노드의 원소 10과 오른쪽 자식 노드인 3번 노드의 원소 26을 더한 36을 저장하고 있다. 그러면 2번 노드와 3번 노드는 무엇을 나타낼까? 2번 노드 또한 왼쪽 자식 노드인 4번 노드의 원소 3과 오른쪽 자식 노드인 5번 노드의 원소 7을 더한 10을 저장하고 있다. 여기서 4번 노드는 1과 2를 더한 3을 저장하고 5번 노드는 3과 4를 더한 7을 저장하고 있는 것을 알 수 있는데, 이를 통해 2번 노드의 원소인 10이라는 숫자는 1,2,3,4를 더한 값 즉, 1번째 원소부터 4번째 원소까지의 구간 합이 저장되어 있다는 것을 알 수 있다. 비슷하게 3번 노드의 원소인 26은 5,6,7,8을 더한 값 즉, 5번째 원소부터 8번째 원소까지의 구간 합을 의미한다. 다시 한번 1번 노드를 생각해 보면 이제 쉬울 것이다. 1번 노드의 36은 1번째 원소부터 4번째 원소까지의 구간 합인 10과 5번째 원소부터 8번째 원소까지의 구간 합이 26을 더한 값이므로 1번째 원소부터 8번째 원소까지의 구간 합을 의미한다.

만약 여기서 5번째 원소인 5를 9로 update 하고 싶으면 어떻게 해야 할까? 일단 5를 9로 바꿔보자!

위와 같이 5를 9로 update 했을 때 영향을 미치는 곳은 어디일까? 그림만 봐도 쉽게 알 수 있다. 바로 6번 노드, 3번 노드, 1번 노드이다. 왜냐하면 이 노드들은 5번째 원소를 포함하는 구간 합 정보를 저장하고 있기 때문이다. 그러면 5번째 원소인 5가 9로 update 했다면 이 노드들 또한 아래와 같이 알맞게 update 해주면 될 것이다.

하나만 더 바꿔 보자. 첫 번째 원소인 1을 11로 바꿔보면 아래와 같이 바뀔 것이다.

이제 구현을 해보자. 한 원소를 update 했을 때 어떤 노드들을 update 해야 할까? 위의 예시를 다시 들여다보자.

5번째 원소 5를 저장하는 12번 노드를 update 했더니 6번 노드, 3번 노드, 1번 노드가 update 되었다.

1번째 원소 1을 저장하는 8번 노드를 update 했더니 4번 노드, 2번 노드, 1번 노드가 update 되었다.

이제 좀 감이 올 것이다. 바로 변경한 노드부터 루트 노드까지 부모 노드를 따라 올라가면서 update 된다는 것을 알 수 있다. 부모 노드의 인덱스는 자식 노드의 인덱스에 2를 나눈 값이라고 했으므로 처음 변경한 인덱스에서 루트 노드 즉, 인덱스가 1이 될 때까지 2를 나누면서 해당하는 노드의 원소를 update 해주면 되는 것이다. 일단 아래 코드를 보자.

// idx번째 원소를 num으로 update
void update(int idx, int num) {
	idx += OFFSET;
	tree[idx] = num;
   	// idx가 1이 될 때까지 update
	while (idx > 1) {
		idx /= 2;
		tree[idx] = tree[idx * 2] + tree[idx * 2 + 1];
	}
}

idx번째 원소를 num으로 update 하고 싶다는 함수이다. 3번째 line에서 idx에 $OFFSET$을 더해주었다. 왜냐하면 idx번째 원소는 인덱스 트리에서 $OFFSET$ + idx번 노드를 나타내기 때문이다. 4번째 line에서 일단 idx번 노드를 update해준 다음 while문에 들어간다. idx가 루트 노드 즉, 1이 될 때까지 2를 나눠가면서 해당하는 노드의 원소를 update 한다. 원소를 update 할 때는 init 함수와 똑같이 왼쪽 자식 노드의 원소와 오른쪽 자식 노드의 원소를 더한 값을 저장해 주면 된다!

idx번 노드부터 루트 노드까지 부모 노드를 따라 올라가면서 원소를 update 해주기 때문에 트리의 높이만큼 시간이 소요된다. 이 때문에 시간복잡도가 $O(logN)$이 되는 것이다.

4) Range query

이제 구간 합을 구해보자. (사실 잘 설명할 수 있을지 모르겠다...)

각각의 노드에 저장된 원소가 어떤 값을 의미하는지는 알아보았다. 그런데 만약 노드에 저장된 원소가 의미하지 않는 구간 합을 알고 싶다면 어떻게 해야 할까? 예를 들어 5번째 원소부터 8번째 원소까지의 구간 합은 3번 노드의 원소인 26으로 바로 구할 수 있지만, 4번째 원소부터 7번째 원소까지의 구간 합을 저장하고 있는 노드는 없기 때문이다.

4번째 원소부터 7번째 원소까지의 구간 합은 [ 4번째 원소 + 5번째 원소부터 6번째 원소까지의 구간 합 + 7번째 원소 ]로 분리할 수 있다. 4번째 원소는 11번 노드에 저장되어 있고, 5번째 원소부터 6번째 원소까지의 구간 합은 6번 노드에 저장되어 있으며 7번째 원소는 14번 노드에 저장되어 있기 때문에 11번 노드 원소 4 + 6번 노드 원소 11 + 14번 노드 원소 7 = 22로 구할 수 있다.

하나만 더 해보자. 2번째 원소부터 8번째 원소까지의 구간 합은 어떻게 분리할 수 있을까? [ 2번째 원소 + 3번째 원소부터 4번째 원소까지의 구간 합 + 5번째 원소부터 8번째 원소까지의 구간 합 ]으로 분리할 수 있을 것이다. 2번째 원소를 저장하는 9번 노드와 3번째 원소부터 4번째 원소까지의 구간 합을 저장하는 5번 노드와 5번째 원소부터 8번째 원소까지의 구간 합을 저장하는 3번 노드를 모두 더한 35가 답이 될 것이다.

그렇다면 예시처럼 구간을 분리하는 기준을 무엇일까? A번째 원소부터 B번째 원소까지의 구간 합을 구한다고 해보자. A번째 원소를 저장하는 노드는 A +$OFFSET$번 노드이고 B번째 원소를 저장하는 노드는 B + $OFFSET$번 노드이지만 편하게 설명하기 위해서 A번 노드, B번 노드라고 하겠다.

구간을 분리하는 기준은 결론부터 말하면 A번 노드와 B번 노드가 왼쪽 자식 노드인지 오른쪽 자식 노드인지에 따라 기준이 나뉜다. 정확히는 A번 노드가 오른쪽 자식 노드일 때와 B번째 노드가 왼쪽 자식 노드일 때 구간이 분리된다. 기본적으로 A번 노드와 B번 노드를 각각 부모 노드로 올리면서 노드에 저장되어 있는 원소를 적절히 더하며 구간 합을 구하는 것인데, A번 노드와 B번 노드가 어떤 쪽 자식 노드인지가 부모 노드로 올리는 기준이 된다. A번 노드가 왼쪽 자식 노드이고 B번 노드가 오른쪽 자식 노드라면 부모 노드로 올릴 수 있지만, A번 노드가 오른쪽 자식 노드이거나 B번째 노드가 왼쪽 자식 노드인 경우에는 인덱스 트리에서 더 이상 부모 노드로 올리면 안 된다. 만약 이 경우에 부모 노드로 올라가 버린다면 내가 구하고 싶지 않은 구간을 포함해 버리게 되기 때문이다.

예를 들어 아래 인덱스 트리에서 4번째 원소부터 7번째 원소까지의 구간 합을 구한다고 해보자.

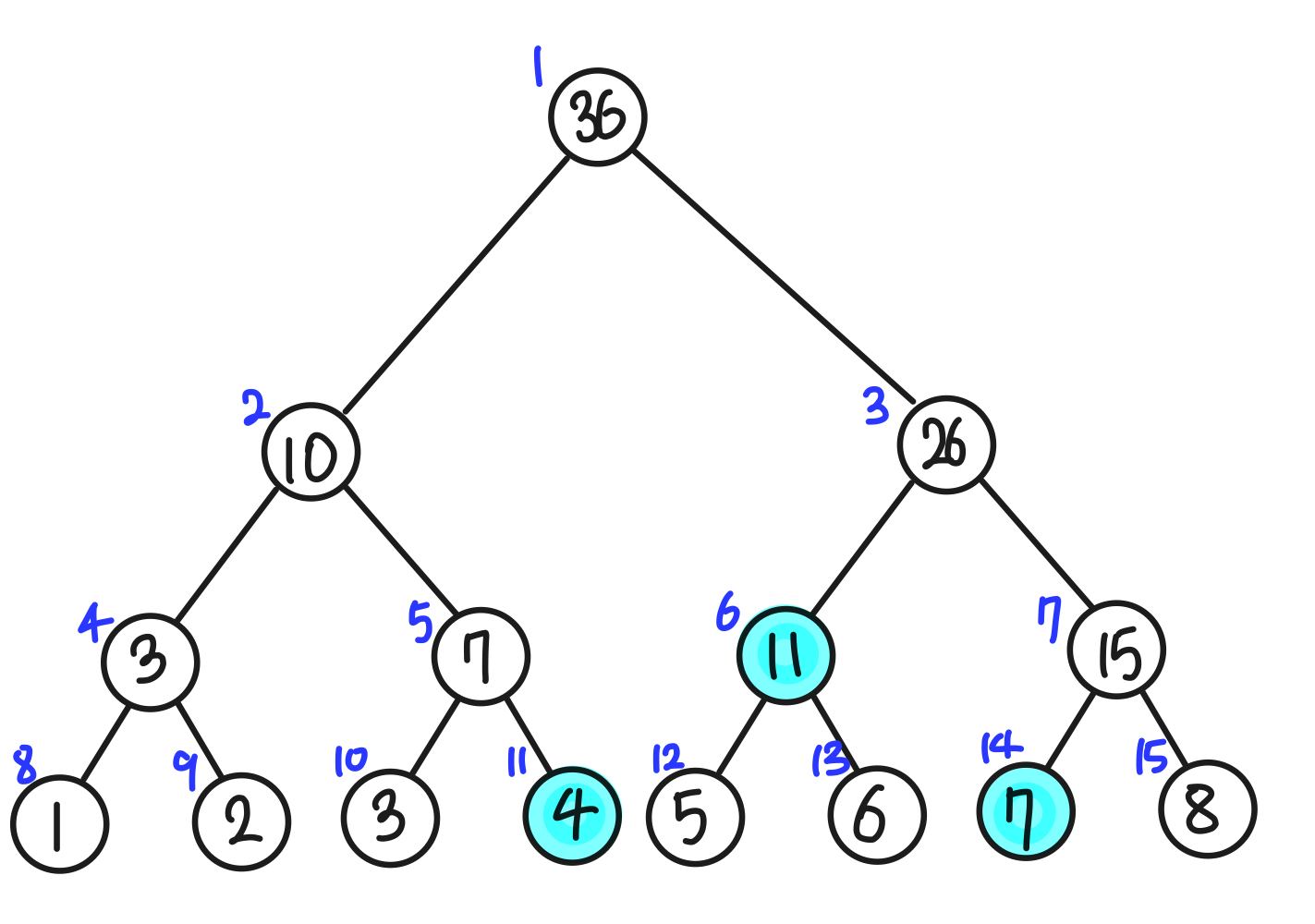
일단 4번째 원소를 저장하는 노드는 11번 노드이고 7번째 원소를 저장하는 노드는 14번 노드이므로 4번째 원소부터 7번째 원소까지의 구간 합을 11번 노드부터 14번 노드까지의 합이라고 생각해 보자. 11번 노드는 오른쪽 자식 노드이므로 11번 노드에서 더 이상 부모 노드로는 올라가면 안 된다는 뜻이다. 왜냐하면 11번 노드의 부모 노드인 5번 노드는 3번째 원소와 4번째 원소의 합이 저장되어 있는데, 내가 구하고 싶은 구간은 4번째부터 7번째이기 때문에 내가 구하고 싶지 않은 3번째 원소를 포함해 버리기 때문이다. 따라서 11번 노드에서 구간을 분리해야 한다. 14번 노드는 왼쪽 자식 노드이므로 마찬가지로 더 이상 부모 노드로 올라가면 안 되고 구간을 분리해야 한다. 이렇게 구간을 분리하면 [ 11번 노드 ] + [ 12~13번 노드 합 ] + [ 14번 노드 ] 이렇게 구간이 분리되는 것을 알 수 있다. [ 12~13번 노드 합 ]은 6번 노드에 저장되어 있으므로 이제 계산을 할 수 있다.

일단 구간이 분리되는 기준은 알았는데 구간 합은 어떻게 구하는 것인지 아직도 감이 안 올 수 있다. 구간 합은 바로 구간이 분리될 때 노드에 저장되어 있는 원소를 더해주면 된다. 아래 예시를 보자.

위 그림은 2번째 원소부터 8번째 원소까지의 구간 합을 구할 때 구간이 분리되는 지점을 색칠한 인덱스 트리다. 2번째 원소부터 8번째 원소까지의 구간 합은 9번 노드부터 15번 노드까지의 합으로 생각할 수 있다. 차근차근 구간 합을 구해 보자.

1. [ 9~15번 노드 합 ]

- 9번 노드 : 오른쪽 자식 노드 & 15번 노드 : 오른쪽 자식 노드 => 구간 분리 : [ 9번 노드 ] + [ 10~15번 노드 합 ]

2. [ 10~15번 노드 합 ]

- 10번 노드 : 왼쪽 자식 노드 & 15번 노드 : 오른쪽 자식 노드 => 부모 노드 올리기 : [ 5~7번 노드 합 ]

3. [ 5~7번 노드 합 ]

- 5번 노드 : 오른쪽 자식 노드 & 7번 노드 : 오른쪽 자식 노드 => 구간 분리 : [ 5번 노드 ] + [ 6~7번 노드 합 ]

4. [ 6~7번 노드 합 ]

- 6번 노드 : 왼쪽 자식 노드 & 7번 노드 : 오른쪽 자식 노드 => 부모 노드 올리기 : [ 3번 노드 ]

위 식을 한 번에 정리하면 다음과 같다.

[ 9~15번 노드 합 ] = [ 9번 노드 ] + [ 10~15번 노드 합 ]

= [ 9번 노드 ] + [ 5~7번 노드 합 ]

= [ 9번 노드 ] + [ 5번 노드 ] + [ 6~7번 노드 합 ]

= [ 9번 노드 ] + [ 5번 노드 ] + [ 3번 노드 ]

= 2 + 7 + 26 = 35

이제 구현을 해보자. 코드는 아래와 같다.

// left번째 원소부터 right번째 원소까지 구간 합
int query(int left, int right) {
	int ret = 0;
	left += OFFSET, right += OFFSET;
    	// left가 right보다 커질 때까지
	while (left <= right) {
    		// 구간 나누기
		if (left % 2 == 1) ret += tree[left++]; // left가 오른쪽 자식일 때
		if (right % 2 == 0) ret += tree[right--]; // right가 왼쪽 자식일 때
        	// 부모로 올리기
		left /= 2, right /= 2;
	}
	return ret;
}

함수에서 반환할 리턴값을 ret라고 선언하고 0으로 초기화 한 다음 시작한다. 4번째 line은 update 함수와 마찬가지로 실제 인덱스 트리에서 left번째 원소와 right번째 원소를 저장하고 있는 노드를 가리키기 위해 각각 $OFFSET$을 더하는 것이다.

while문은 left가 right보다 커질 때까지 실행되는데 이것은 left와 right가 부모 노드로 올라가다가 같은 부모 노드를 가리키면 while문이 종료된다는 것을 의미한다.

8~9번째 line은 left가 오른쪽 자식 노드이거나 right가 왼쪽 자식 노드인 경우를 의미한다. 인덱스 트리에서 왼쪽 자식 노드는 항상 짝수이고 오른쪽 자식 노드는 항상 홀수이다. 따라서 [ left % 2 == 1 ]과 [ right % 2 == 0 ]으로 left와 right가 각각 어느 쪽 자식인지 판단할 수 있다. 구간을 분리하는 것은 left를 1 증가시키거나 right를 1 감소시키는 것으로 구현할 수 있다. 구간을 분리하는 동시에 ret값에 현재 노드에 저장하고 있는 원소값을 더해준다.

11번째 line은 현재 노드를 부모 노드로 올리는 경우를 의미하는데 부모 노드는 항상 자식 노드의 2를 나눈 값이므로 left와 right를 각각 2를 나눠주는 것으로 구현할 수 있다.

구간 합을 구하는 것 또한 최악의 경우일 때 트리의 높이만큼 시간이 소요되므로 시간복잡도가 $O(logN)$이 되는 것이다.

3. 전체 코드

// OFFSET 설정
int OFFSET = 1; // 1부터 시작
while (OFFSET < N) OFFSET *= 2; // N보다 크거나 같아질 때까지 2배

// 인덱스 트리 배열 설정
vector<int>tree(OFFSET * 2);

// 초기화 함수
void init() {
	// OFFSET부터 OFFSET + N - 1 까지
	for (int i = 0; i < N; i++) tree[i + OFFSET] = arr[i];
	// 1부터 OFFSET - 1 까지
	for (int i = OFFSET - 1; i >= 1; i--) tree[i] = tree[2 * i] + tree[2 * i + 1];
}

// idx번째 원소를 num으로 update
void update(int idx, int num) {
	idx += OFFSET;
	tree[idx] = num;
	// idx가 1이 될 때까지 update
	while (idx > 1) {
		idx /= 2;
		tree[idx] = tree[idx * 2] + tree[idx * 2 + 1];
	}
}

// left번째 원소부터 right번째 원소까지 구간 합
int query(int left, int right) {
	int ret = 0;
	left += OFFSET, right += OFFSET;
	// left가 right보다 커질 때까지
	while (left <= right) {
		// 구간 나누기
		if (left % 2 == 1) ret += tree[left++]; // left가 오른쪽 자식일 때
		if (right % 2 == 0) ret += tree[right--]; // right가 왼쪽 자식일 때
		// 부모로 올리기
		left /= 2, right /= 2;
	}
	return ret;
}